最近在读 SYSU 郑伟诗老师关于 Person Re-Identification 论文, 这里是一些笔记. 读的几篇论文都是从 Metric Learning 的角度来处理重识别问题. 写得比较粗略, 有很多细节还不是特别清楚, 先挖个坑, 之后再来填.
Pipeline
这篇论文提出了一个称为 CRAFT 的 framework, 首先使用神经网络进行特征提取初级特征, 并进行 View-specific 的特征增强和特征空间映射. 特征提取部分主要是用到了 AlexNet 的浅层部分, 利用已有网络进行特征提取的思路其实用得很多了现在, 在例如风格迁移, 迁移学习等方面都有涉及. 具体提取流程如下

特征提取
首先进行特征提取, 论文中提出的方法被称为 HIPHOP, 提取过程如下.
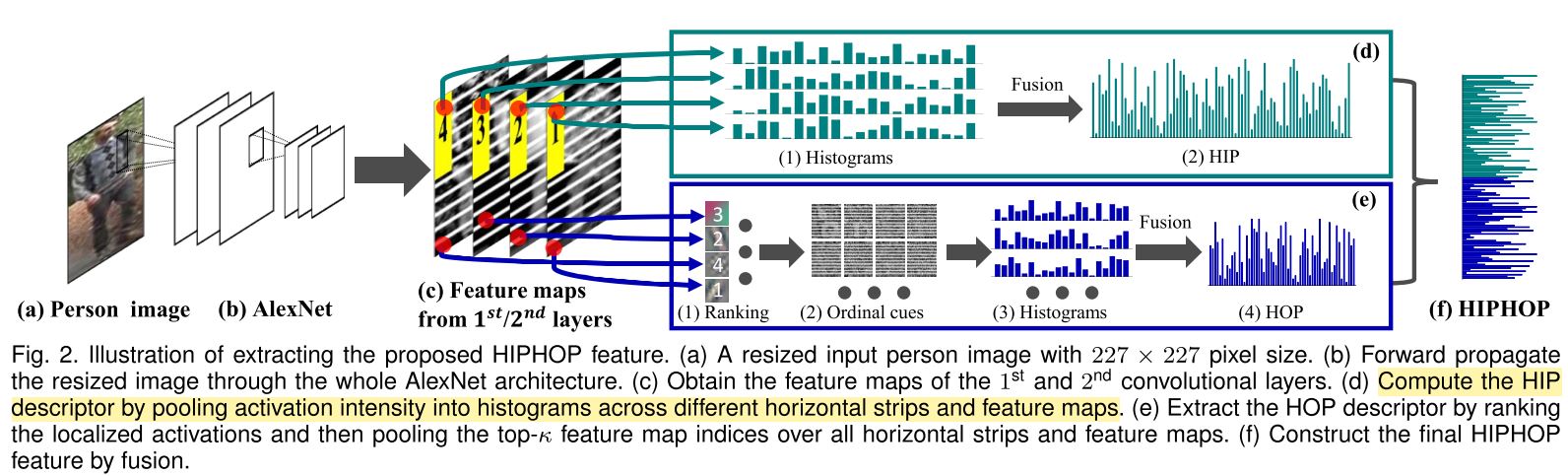
将 feature map 分解成水平的条纹 (高度固定为 5) 来进行特征结构提取. HIP 特征将多个条纹的直方图拼接到一起来得到. HOP 特征则提取 feature map 中响应最大的 \( k \) 个神经元 (这里为 20) 的值来提取直方图. 最后融合 HIP 和 HOP 特征.
之所以使用低层次特征, 是因为高层次特征具有较大的感受野, 容易在人体姿势或背景剧烈变化时被改变 (contaminated), 因此不适合进行比较 Person Re-ID, 相对来说 Person Re-ID 是比较局部化的.
CRAFT
进行 view-specific augmentation 需要 1) 量化不同视角的差异程度, 使用 principle 作为度量标准, 可以粗糙地理解为两个子空间的夹角余弦值. 2) 从相似度提取 augmentation 所需的信息, 即 camera correlation. 公式如下
\[\omega=\frac{1}{r} \sum_{k=1}^{r}\cos(\theta_k)\]其中 \( \theta_k \) 为 principle angle, 可以粗略地理解为两个子空间的夹角.
论文中的 feature augmentation 的方法基于一种补零的方法 (可以理解为通过升维来匹配数据分布), 但补零的方法是 camera-generic 的, 论文对补零的方法进行推广, 如果补零的方法表示为
\[\tilde{\boldsymbol{X}}_{\text{zp}}^a=\begin{bmatrix} \boldsymbol{I}_{d\times d} \\ \boldsymbol{O}_{d\times d} \end{bmatrix} \boldsymbol{X}^b, \quad \quad \tilde{\boldsymbol{X}}_{\text{zp}}^b=\begin{bmatrix} \boldsymbol{O}_{d\times d} \\ \boldsymbol{I}_{d\times d} \end{bmatrix} \boldsymbol{X}^b\]则推广的 camera-specific augmentation 使用下式
\[\tilde{\boldsymbol{X}}_{\text{zp}}^a=\begin{bmatrix} \boldsymbol{R} \\ \boldsymbol{M} \end{bmatrix} \boldsymbol{X}^a, \quad \quad \tilde{\boldsymbol{X}}_{\text{zp}}^b=\begin{bmatrix} \boldsymbol{M} \\ \boldsymbol{R} \end{bmatrix} \boldsymbol{X}^b\]\( a,b \) 表示两个不同的摄像头. 这样, 在之后进行特征空间映射时, 摄像头之间的互相关信息就能够被考虑进去, 如下式所示
\[f_a(\tilde{\boldsymbol{X}}_{\text{zp}}^a)=\boldsymbol{W}^T\tilde{\boldsymbol{X}}_{\text{zp}}^a=(\boldsymbol{R}^T\boldsymbol{W}^a+\boldsymbol{M}^T\boldsymbol{W}^b)\boldsymbol{X}^a \\ f_b(\tilde{\boldsymbol{X}}_{\text{zp}}^b)=\boldsymbol{W}^T\tilde{\boldsymbol{X}}_{\text{zp}}^b=(\boldsymbol{M}^T\boldsymbol{W}^a+\boldsymbol{R}^T\boldsymbol{W}^b)\boldsymbol{X}^b\]事实上论文中所使用的的 \(\boldsymbol{R,M}\) 的形式其实很简单, 只与 \(\omega \) 有关
\[\boldsymbol{R}=\frac{1-r}{z} \boldsymbol{I} \\ \boldsymbol{M}=\frac{1+r}{z} \boldsymbol{I} \\ z = \sqrt{(1-r)^2+(1+r)^2}\]同样地, 考虑到实际摄像头之间的关联性很强, 论文添加了一个正则化项
\[\|\boldsymbol{W}^a-\boldsymbol{W}^b \|^2\]思考
矩阵 \(R,M\) 是通过 hand-crafted 的方法设计出来的, 是否可以通过某种学习的方法来获得?