概述

深度学习顶会 ICLR 2018 中的一篇高分论文 On the convergence of Adam and beyond 分析了 Adam 优化算法存在的问题并提出了一种改进, 本文结合该论文对深度学习的优化算法做了一个概要性的总结.

学习算法和学习率在深度学习模型的训练 (炼丹) 中扮演者举足轻重的角色, 有时候甚至可能因为没有选对学习算法而不能发挥模型的性能, 这时候满以为是模型的问题, 去改变模型, 可能仍然达不到很好的效果. 有时候很难复现论文中的模型性能, 也可能是论文作者在训练模型的时候使用了一些黑科技.

在深度学习中面对的优化目标往往都是非常高维且是非凸的, 因此不可能通过直接求导并令导数为 0 来得到最优点, 我们可以把优化目标函数想象成沟壑纵横的丘陵, 想找到最低点, 只能通过走一步看一步的方法来探索, 而且由于二阶梯度的计算量巨大, 我们通常只能使用一阶梯度或者二阶梯度的近似 (我们这里只讨论使用一阶梯度的情况), 这就是说, 我们只能知道当前所在点的梯度信息, 而不知道梯度的变化情况. 这个过程有两个主要要决定的量, 即前进的方向和前进的步长. 方向可以通过观察周围的坡度 (梯度) 来决定, 而步长 (学习率), 就不太好确定了.

许多优化算法先后被提出, 训练模型因此也容易了许多. 这些方法的基本思想都是根据之前的梯度来自适应调整下降方向和学习速率, 方法主要是通过梯度的指数滑动平均来保留之前的梯度, 如果最近的梯度一直都很大, 那么说明这个方向很可能正确的, 所以可以增大学习速率, 反之, 当梯度变化较大时, 我们期望网络能够更加谨慎地改变参数.

之前算法的问题在于并不能保证收敛到一个比较好的值. 在一些情况下, 只有部分 mini bathch 提供了很大的梯度, 但由于指数加权的作用, 这些信息量大的 mni batch 的影响很快就被削弱, 因此最终导致收敛于一个差的收敛点.

算法框架

优化算法的一般流程可以表示为

算法框架

其中

\[\phi_t: \mathcal{F}^t \to \mathbb{R}^d \\ \psi_t: \mathcal{F}^t \to \mathcal{S}_+^d \\ \alpha_t = \alpha / \sqrt{t}\]

\( \mathcal{F} \) 为参数的可行域, \(\mathcal{S}_+^d \) 表示所有正定矩阵的集合 (在这里我们一般要求它是对角的). 这两个函数是自适应算法的关键, 直观地可以理解为某种在梯度上取平均的函数.

基于 SGD 的算法

对于 SGD, 有 \(\phi_t(g_1, \ldots, g_t)=g_t\) 和 \(\psi (g_1,\ldots, g_t)=\mathbb{I}\). 如果学习率衰减, 则有 \(\alpha_t=\alpha/\sqrt{t}\). SGD 是最简单原始的梯度下降方法, 但这种方法还是被广泛应用. 这种方法沿着梯度的方向按预先给定的步长来进行.

如果在 SGD 中的 \(\phi\) 中加入一阶矩, 便是 SGD-M (SGD with Momentum). 即 \( \phi(g_1, \ldots, g_t)=(1-\beta_1)\sum_{i=1}^t \beta_1^{t-i}g_i\). 实际上这可以通过递归来实现 \( m_{t+1}=\beta_1m_t+(1-\beta_1)g_t) \). 使用了动量 (一阶矩) 可以有效避免学习速率方向的震荡, 可以想象, 当穿越谷地时, 使用动量可以避免参数.

另一种方法是所谓的 Nesterov (NAG), 它的区别在于 \( g_t=\nabla f(x_t-\alpha_tm_t\sqrt{V_t}) \), 即使用下一点的梯度来决定当前的方向, 使学习具有预见性.

对于 AdaGrad , 不同点在于 \(\psi(t)(g_1, \ldots, g_t)=\frac{\text{diag}(\sum_{i=0}^t g_i^2)}{{t}}\). 使用二阶矩能够有效控制学习率, 防止学习率的震荡.

学习率单调递减, 但是有可能使得学习速率过快地衰减为 0, 导致不收敛. 在稀疏梯度的情况下能运行得很好.

自适应算法

自适应的算法主要有 RMSProp, AdaDelta, Adam, NAdam.

RMSProp 继承了 AdaGrad 的思想, 在 \(V_t \) 中累计梯度的二阶矩, 但做法更为优雅 (和 AdaGrad 将所有的梯度平方和累加起来相比), 它是使用滑动平均的方式进行积累, 使过去太久的梯度的作用减小, 减少学习率过快衰减而不收敛的风险, 但也同样能够稳定学习速率.

Adam 可以说是以上几种思想的集大成者, 有 \( \phi_t(g_1, \ldots, g_t)=(1-\beta_1) \sum_{i=1} ^t \beta_1^{t-i}g_i \) 和 \( \psi_t(g_1, \ldots, g_t)=(1-\beta_2)\text{diag}(\sum_{i=1}^t \beta_{2}^{t-i}g_i^2\). RMSProp 是其 \(\beta_1=0 \) 的特例. 一般来说 \(\beta_1 \) 的推荐值是 \(0.9 \), \(\beta_2 \) 为 \(0.999\). 另外论文中其实漏了一个修正项, 即

\[m_t \leftarrow m_t/(1-\beta_1^t) \\ V_t \leftarrow V_t/(1-\beta_2^2)\]

这样可以避免在开始时, \(m_t, V_t\) 过小的问题.

而所谓的 NAdam 就是 Nesterov + Adam 了.

关于这些算法的性能, 可以看下面的动态图

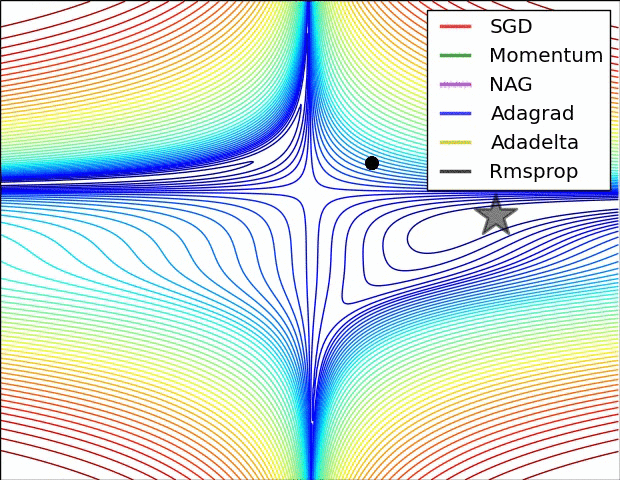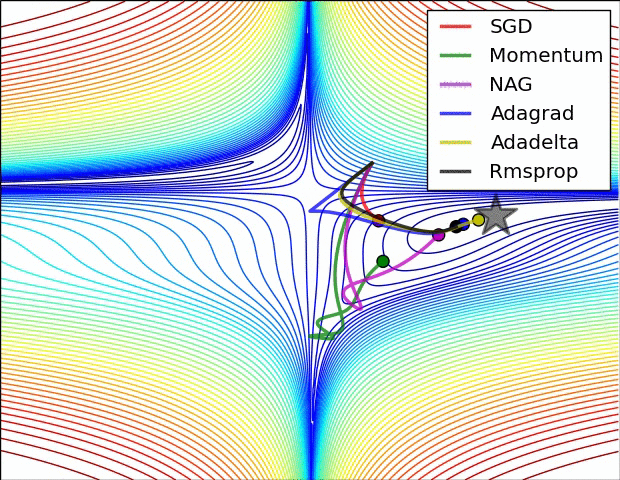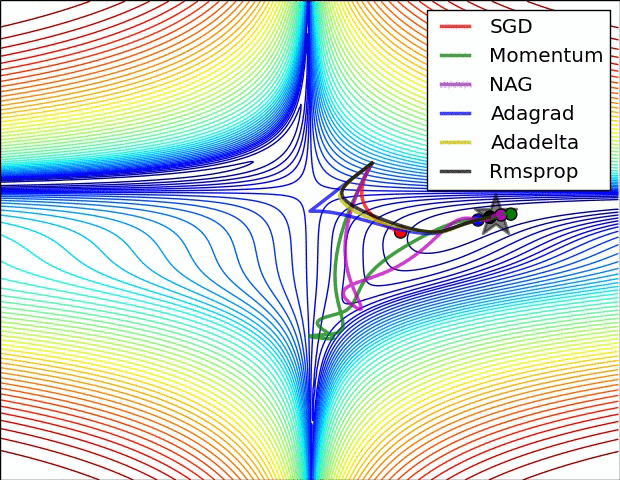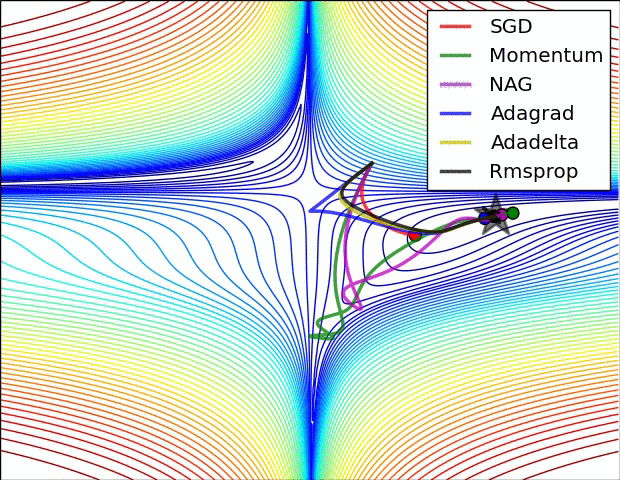
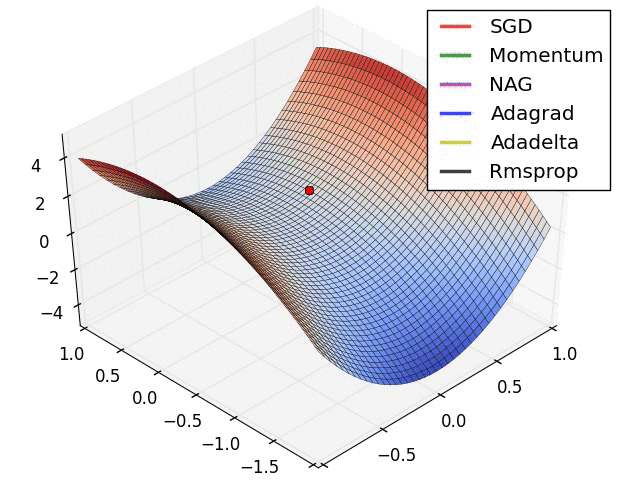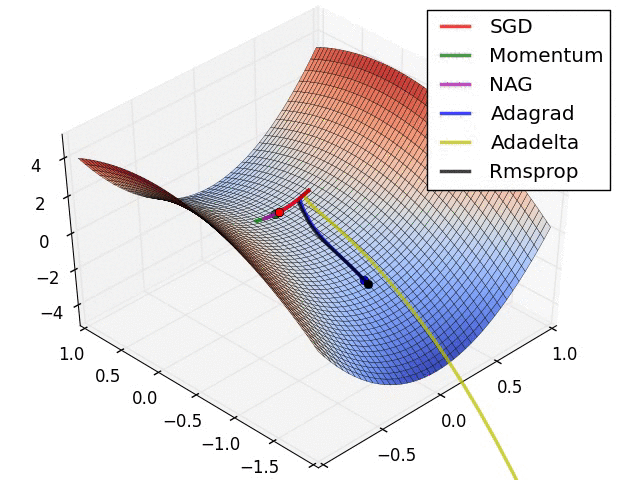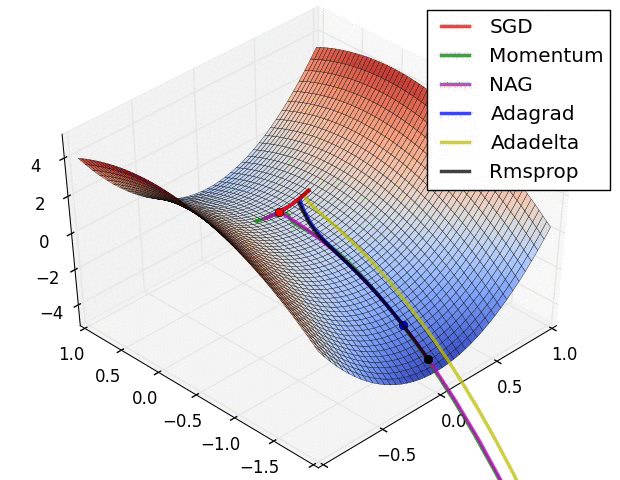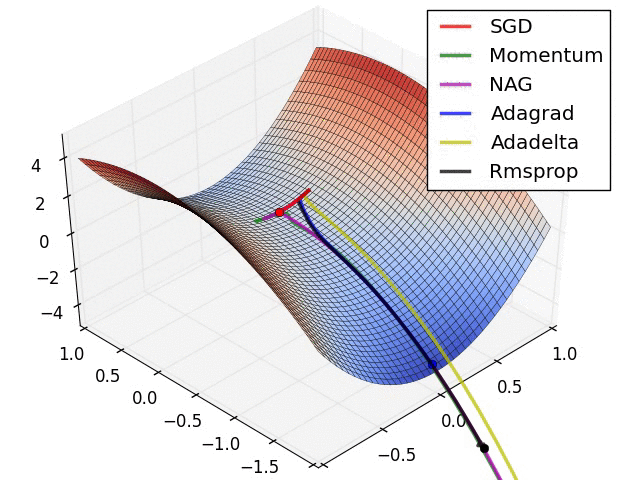
对于 SGD 和 AdaGrad, 可以保证学习率总是衰减的, 而基于滑动平均的方法则未必. 实际上, 以 Adam 为代表的自适应算法存在两个主要问题:

  • 可能不收敛
  • 可能收敛于局部最优点 (吸引盆)

论文 [3] 分析了 Adam 可能不收敛的情况. 考虑优化下面的函数

\[f_t(x)= \begin{cases} Cx, & \text{for } t \mod 3=1 \\ -x, & \text{otherwise} \end{cases}\]

假设 \(x\) 的可行域为 \(x \in [-1,1]\), \(C>2\). 优化时, 每三次梯度中有一次获得一个大的梯度, 有一次获得小梯度, 且方向相反. 因此可以想到, 其平衡点会在 \(x=-1 \) 处. 然而当 \(\beta_2=\frac{1}{C^2+1}\) 时, Adam 算法将收敛于 \(x=+1\), 这是因为二阶矩的存在, 使得梯度为 \(C\) 时被放缩了一个接近 \(C\) 的因子.

AMSGRAD

论文针对 Adam 中存在的问题进行了改进, 提出 AMSGRAD 算法.

通过取最大值这一步, 保证了学习速率的递减.

建议

实践证明, Adam 虽然收敛得比较快, 但最终收敛的结果并没有 SGD 好[3], 主要是因为后期 Adam 的学习速率较低, 之后实验人员对 Adam 学习速率的下界进行了控制, 发现结果确实好了很多.

基于前面所提到的缺点, 要精调网络达到 state of art 水平, 通常还是得用 SGD. 当然可以在开始的时候使用 Adam, 充分利用 Adam 的快速, 等收敛到一定程度以后再换成 SGD. 但是要注意太晚切换的话, Adam 已经收敛到局部最小点的话, SGD 再好也无可奈何了. 有一篇论文专门讲从 Adam 切换到 SGD 的方法.

Adam等自适应学习率算法对于稀疏数据具有优势, 且收敛速度很快; 但精调参数的SGD (+Momentum) 往往能够取得更好的最终结果.

The two recommended updates to use are either SGD+Nesterov Momentum or Adam）–cs231n

事实上没有万能的模型, 也没有放之四海的优化方法, 还是要根据实际的任务和面对的数据来选择合适的方法.

其他 tricks

  • 数据一定要进行充分的 shuffle, 使特征均匀, 避免某些特征集中出现.
  • 先在小数据集上进行参数搜索, 这是基于下面的事实

    The mathematics of stochastic gradient descent are amazingly independent of the training set size. In particular, the asymptotic SGD convergence rates are independent from the sample size.

参考资料